Universal Properties

Updated: 2021-02-01

Introduction

  • Cartesian Products. Given sets \(A\) and \(B\) their cartesian product \(A \times B\) induces two functions \(\pi_1 : A \times B \mto{} A\) and \(\pi_2 : A \times B \mto{} B\) called the projection maps. Using these projections we can state a useful property of cartesian products. Suppose we have functions \(f : C \mto{} A\) and \(g : C \mto{} B\) for some arbitrary set \(C\). Then there is a unique function \(\langle f,g \rangle : C \mto{} A \times B\) such that the following hold:

    \[ \begin{array}{lll} \langle f,g \rangle;\pi_1 = f\\ \langle f,g \rangle;\pi_2 = g \end{array} \]

    This property can be summed up as the following diagram:

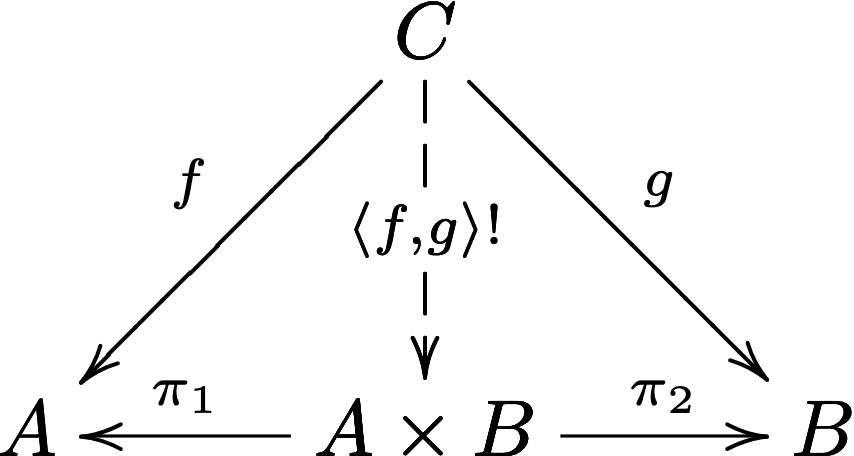
    Commutative diagram of the universal property for products in the category of sets and functions.

    The dotted line stands for there exists and the bang (exclamation mark) stands for unique.

    Notice that we have not given the definition of \(\langle f,g \rangle\), but only its defining property, but this property implies that \(\langle f,g \rangle\) must be defined to be:

    \[ \begin{array}{lll} \langle f,g \rangle : C \mto{} A \times B\\ \langle f,g \rangle(c) = (f(c),g(c)) \end{array} \]

    Thus, this property gives us a way to pair functions with a common domain, and this pairing acts the way we expect it to act when we run it on some elements.

  • Meets in Preorders. Suppose we have a preorder \((P,\leq)\). Then we say that the preorder \((P,\leq)\) has meets if given two elements \(p,q \in P\), there is an element \(p \land q \in P\) such that:

    • \((p \land q) \leq p\)
    • \((p \land q) \leq q\)
    • If \(r \leq p\) and \(r \leq q\), then \(r \leq (p \land q)\)

    Recall that if we treat the preorder \((P,\leq)\) as a category then we take \(P\) as the set of objects, and there is a morphism \(p \mto{f} q\) if and only if \(p \leq q\). Thus, every homset \(\Hom{P}{p}{q}\) has at most one morphism in it. Using this perspective we can recast the definition of meets in categorical terms. It says, for any two objects \(p\) and \(q\) there is an object \(p \land q\) with two projection maps \((p \land q) \mto{\pi_1} p\) and \((p \land q) \mto{\pi_2} q\) such that for any object \(r\), if there are morphisms \(r \mto{f} p\) and \(r \mto{g} q\) there is a unique morphism \(r \mto{\langle f,g \rangle} p \land q\).

    Using this definition of meets we can prove two facts:

    1. Given morphisms \(r \mto{f} p\) and \(r \mto{g} q\), \(\langle f,g \rangle;\pi_1 = f\).
    2. Given morphisms \(r \mto{f} p\) and \(r \mto{g} q\), \(\langle f,g \rangle;\pi_2 = g\).

    We can sum all of this up into the following diagram. A preorder, \((P,\leq)\), has meets if for any two objects \(p,q \in P\), there is an object \((p \land q) \in P\) such that the following diagram commutes:

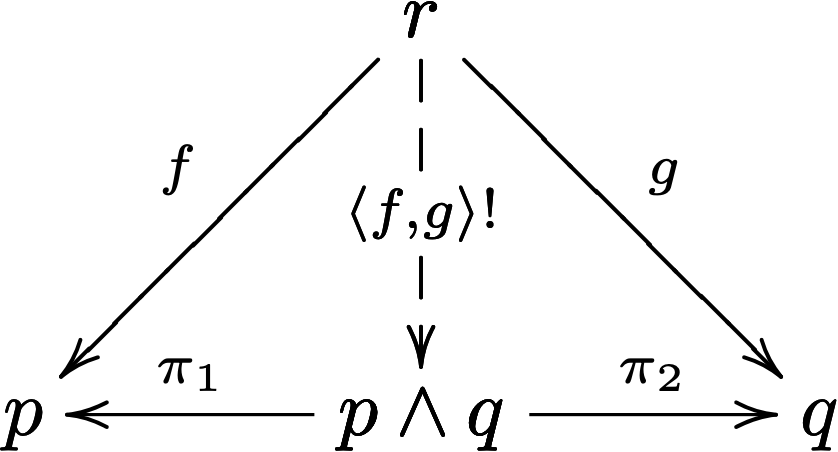
    Commutative diagram of the universal property for binary products in a preorder treated as a category.

    This is the same digram as the first example! Thus, meets in a preorder have the same defining property as cartesian products in sets!

Set-Valued Functors

A functor \(F : \cat{C} \mto{} \sets\) from some category \(\cat{C}\) to the category of sets is called a set-valued functor. It relates objects to sets and morphisms to functions. One can think of them as an interpretation of an abstract category to a concrete category; that is, we can interpret a category without a notion of elements into one with such a notion, and one that we understand quite well.

We give several example set-valued functors below.

  • Suppose \(\cat{C}\) has objects \(\{0,1\}\) and the following morphisms:

    The source and target morphisms defining a directed graph.

    Then a functor \(F : \cat{C} \to \sets\) maps \(1\) to a set \(E\) and \(0\) to a set \(N\), and the two arrows to functions \(s : E \to N\) and \(t : E \to N\). A graph is a tuple \((N,E,s,t)\) where \(N\) is the set of nodes, \(E\) is the set of edge labels, \(s : E \to N\) assigns edges their source nodes, and \(t : E \to N\) assigns edges their target nodes. Therefore, \(F\) represents a graph! In addition, natural transformations between functors like \(F\) correspond to graph homomorphisms (Awodey 2006). Notice that this functor is definable for any category at all, and thus, we can think of a category as an abstraction of a directed graph with a monoid structure given by composition.

  • A monoid \((M, e, \otimes)\) can be thought of as a set-valued functor \(M \ottsym{:} \mathbf{1} \mto{} \mathsf{Set}\) with two natural transformations:

    \[ \begin{array}{lll} \text{(Identity)} & e \ottsym{:} \{ \star \} \mto{} M\\ \text{(Multiplication)} & \otimes \ottsym{:} M \, \times \, M \mto{} M \end{array} \]

    with the following commutative diagrams:

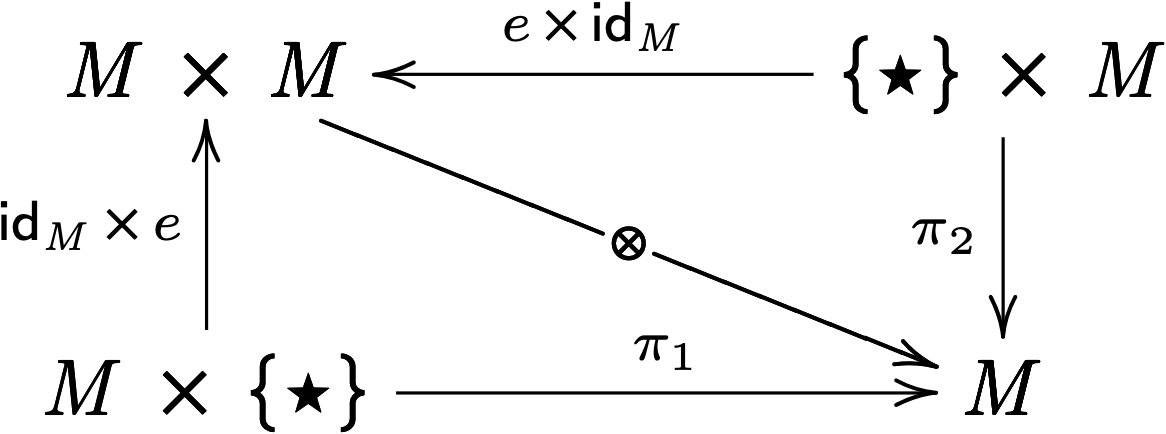
    Commutative diagram for the left and right identity axioms for a monoid.

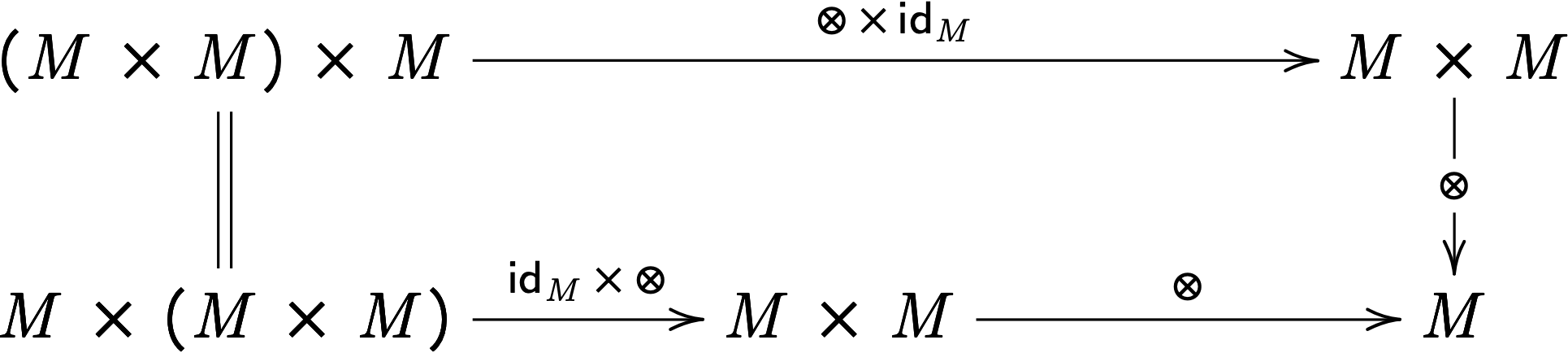
    Commutative diagram for associativity axiom for a monoid.

    The left diagram corresponds to the identity axioms of the monoid, and the right diagram corresponds to associativity of multiplication. In this example, we made use of the following functors:

    \[ \begin{array}{lllllll} \begin{array}{lll} \text{(Singleton Set)}\\ \begin{array}{lll} \{ \star \} \ottsym{:} \mathbf{1} \mto{} \mathsf{Set}\\ \{ \star \}(\bullet) = \{ \star \}\\ \{ \star \}(\mathsf{id} _{ \bullet }) = \mathsf{id} _{ \{ \star \} } \end{array} \end{array} & \quad & \begin{array}{lll} \text{(Product Functor)}\\ \begin{array}{lll} M \, \times \, M \ottsym{:} \mathbf{1} \mto{} \mathsf{Set}\\ ( M \, \times \, M ) \ottsym{(} \bullet \ottsym{,} \bullet \ottsym{)} = M \ottsym{(} \bullet \ottsym{)} \, \times \, M \ottsym{(} \bullet \ottsym{)}\\ ( M \, \times \, M ) \ottsym{(} \mathsf{id} _{ \bullet } \ottsym{,} \mathsf{id} _{ \bullet } \ottsym{)} = \mathsf{id} _{ ( M \ottsym{(} \bullet \ottsym{)} \, \times \, M \ottsym{(} \bullet \ottsym{)} ) }\\ \end{array} \end{array} \end{array} \]

    These are also both examples of set-valued functors. The left functor is essentially the singleton set, and the right functor is the cartesian product of the underlying set of the monoid with itself. Thus, a set-valued functor, \(X \ottsym{:} \mathbf{1} \mto{} \mathsf{Set}\), is a set \(X\) lifted up a level to functors.

  • Suppose we have a monoid \((M, e, \otimes)\). A graded monoid is a set-valued functor \(G \ottsym{:} M \mto{} \mathsf{Set}\) with two natural transformations:

    \[ \begin{array}{lll} \text{(Identity)} & i \ottsym{:} \{ \star \} \mto{} G \ottsym{(} e \ottsym{)}\\ \text{(Multiplication)} & \oast \ottsym{:} G \ottsym{(} \ottmv{r_{{\mathrm{1}}}} \ottsym{)} \, \times \, G \ottsym{(} \ottmv{r_{{\mathrm{2}}}} \ottsym{)} \mto{} G \ottsym{(} \ottmv{r_{{\mathrm{1}}}} \, \otimes \, \ottmv{r_{{\mathrm{2}}}} \ottsym{)} \end{array} \]

    with the following commutative diagrams:

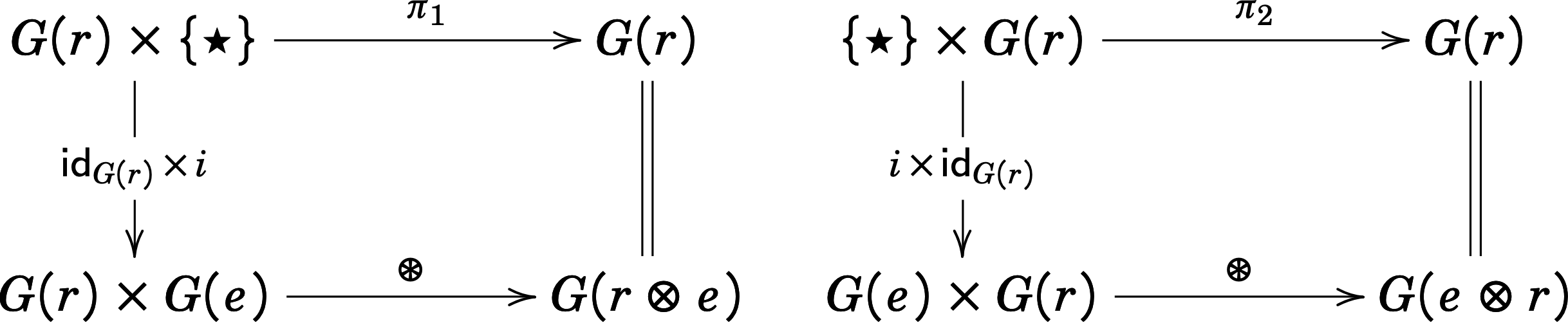
    Commutative diagram for the left-identity axiom for a graded monoid.

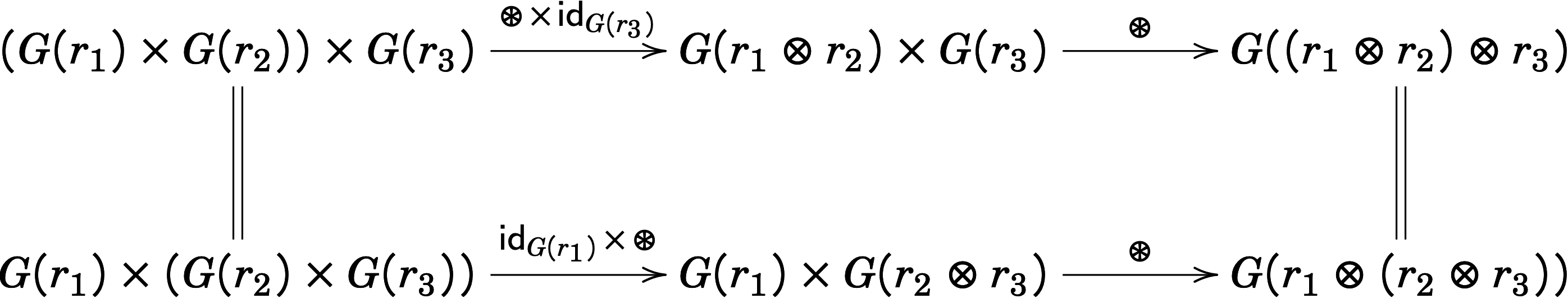
    Commutative diagram for the associativity axiom for a graded monoid.

    The diagrams on top correspond to the identity axioms of the graded monoid, and the diagram on bottom corresponds to associativity of graded multiplication.

    An example graded monoid can be found in formal language theory. Take \(\Sigma^n\) to be all the words of length \(n\) over an alphabet \(\Sigma\). Then \(\Sigma^0\) contains only the empty word, and can be lifted to a map \(\varepsilon : \{ \star \} \mto{} \Sigma^0\), and composition of words lifts to a map \(\cdot : \Sigma^m \times \Sigma^n \mto{} \Sigma^{m + n}\). Thus, since the empty word is the identity of composition of words, and composition is associative up to associativity of addition we have a graded monoid \((\Sigma^{-},\varepsilon, \cdot)\) over the additive natural number monoid \((\mathbb{N},0, +)\). Using this graded monoid we can define the Kleene-star of an alphabet \(\Sigma\) to be \(\Sigma^* = \bigcup_{n \in \mathbb{N}} \Sigma^n\).

  • There is one very important set-valued functor we have seen several times. Suppose \(A\) is an object of the category \(\cat{C}\). Then we can define the covariant hom-set functor:

    \[ \begin{array}{lll} \Hom{C}{A}{-} : \cat{C} \to \sets\\ \Hom{C}{A}{B} = \{f : A \to B \mid f \in \mor{C}\}\\ \Hom{C}{A}{h}(g) = g;h \end{array} \]

    The proof that this is indeed a functor is left as an exercise. In addition, prove that this functor is natural in \(B\).

  • Suppose \(B\) is an object of the category \(\cat{C}\). Then we can define the contravariant hom-set functor:

    \[ \begin{array}{lll} \Hom{C}{-}{B} : \catop{C} \to \sets\\ \Hom{C}{A}{B} = \{f : A \to B \mid f \in \mor{C}\}\\ \Hom{C}{f}{B}(g) = f;g \end{array} \]

    The proof that this is indeed a functor is left as an exercise. In addition, prove that this functor is natural in both \(A\).

  • Suppose \(A\) and \(B\) are objects of the category \(\cat{C}\). Then we can define the hom-set functor:

    \[ \begin{array}{lll} \Hom{C}{-}{-} : \catop{C} \times \cat{C} \to \sets\\ \Hom{C}{A}{B} = \{f : A \to B \mid f \in \mor{C}\}\\ \Hom{C}{f}{h}(g) = f;g;h \end{array} \]

    The proof that this is indeed a functor is left as an exercise. In addition, prove that this functor is natural in both \(A\) and \(B\).

The last three examples are of particular importance, because they underly the definition of a very important class of functors called representable functors.

Representable Functors

Simply put, universal properties are what are called representable functors. These correspond to set-valued functors with a special property that states that they can be completely captured by a collection of morphisms. An example may help make this informal explanation more clear.

Suppose \(X\) is a set. Then we can define the following functions between \(X\) and the set of functions \(\Hom{\mathsf{Set}}{\{ \star \}}{X}\) from the singleton set \(\{ \star \}\) to \(X\):

\[ \begin{array}{lll} \begin{array}{lll} \phi : X \mto{} \Hom{\mathsf{Set}}{\{ \star \}}{X}\\ \phi(x) = \lambda \_.x\\ \end{array} & \begin{array}{lll} \phi^{-1} : \Hom{\mathsf{Set}}{\{ \star \}}{X} \mto{} X\\ \phi^{-1}(f) = f(\star)\\ \end{array} \end{array} \]

The function \(\phi\) is the constant function always returning \(x\), and its inverse takes in a function from \(\{ \star \}\) to \(X\), and simply applies it to its only input. We can easily see that this forms a bijection. Thus, every set \(X\) is in bijection with the set of functions \(\Hom{\mathsf{Set}}{\{ \star \}}{X}\). Now consider the functor \(\mathsf{id} _{ \mathsf{Set} } \ottsym{:} \mathsf{Set} \mto{} \mathsf{Set}\). Using the above argument we can define a natural isomorphism \(\alpha : \Hom{\mathsf{Set}}{\{ \star \}}{-} \mto{} \mathsf{id} _{ \mathsf{Set} }\) by setting \(\alpha_X = \phi^{-1}\).
Functors like \(\mathsf{id} _{ \mathsf{Set} }\) that have such an object like \(\{ \star \}\) that induces a natural isomorphism like \(\alpha\) are called representable functors.

A set-valued functor \(F : \cat{C} \mto{} \sets\) is called representable if and only if there is an object \(A \in \Obj{C}\) and a natural isomorphism \(\alpha : F \mto{} \Hom{C}{A}{-}\). We call the pair \((A,\alpha)\) a representation of \(F\).

The definition just given can be recast into a definition for contravariant set-valued functors \(F : \catop{C} \mto{} \sets\), called presheafs, by proving it naturally isomorphic to the contravariant hom functor.

A set-valued contravariant functor (presheaf) \(F : \catop{C} \mto{} \sets\) is called representable if and only if there is an object \(B \in \Obj{C}\) and a natural isomorphism \(\beta : F \mto{} \Hom{\catop{C}}{-}{B}\). We call the pair \((B,\beta)\) a representation of \(F\).

Let’s consider some example representable functors.

  • The prototypical example of a representable functor is the powerset functor \(\mathcal{P} : \sets^{\mathsf{op}} \mto{} \sets\) defined by

    \[ \begin{array}{lll} \mathcal{P}(X) & = & \{Y \mid Y \subseteq X\}\\ \mathcal{P}(f : B \mto{} A) & = & \lambda X \subseteq A.\{x \in B \mid f(x) \in X\} : \mathcal{P}(A) \mto{} \mathcal{P}(B)\\ \end{array} \]

    We should check that this defines a functor. First we check that identities are preserved:

    \[ \begin{array}{lll} \pow{\id : A \mto{} A} & = & \lambda X \subseteq A.\{x \in A \mid \id(x) \in X\}\\ & = & \lambda X \subseteq A.\{x \in A \mid x \in X\}\\ & = & \lambda X \subseteq A.X\\ \end{array} \]

    Next we check that compositions are preserved. Suppose \(f \in \Hom{\sets^{\mathsf{op}}}{B}{A}\) and \(g \in \Hom{\sets^{\mathsf{op}}}{C}{B}\). Then

    \[ \begin{array}{lll} \pow{g;f : C \mto{} A} & = & \lambda X \subseteq A.\{x \in C \mid f(g(x)) \in X\}\\ & = & \lambda X \subseteq A.\{x \in C \mid f(g(x)) \in X\}\\ & = & \lambda X \subseteq A.\{x \in C \mid g(x) \in \{y \in B \mid f(y) \in X\}\}\\ & = & (\lambda Y \subseteq A.\{y \in B \mid f(y) \in Y\});(\lambda X \subseteq B.\{x \in C \mid g(x) \in X\})\\ & = & \pow{f};\pow{g} \end{array} \]

    To prove that the powerset functor is representable we need to find a representation of it. Thus, we must find a set \(B\) together with a natural isomorphism \(\alpha : \Hom{\sets^{\mathsf{op}}}{-}{B} \mto{} \mathcal{P}\). The most difficult part is finding \(B\). To do this it is helpful to consider how \(\mathcal{P}\) is defined. Suppose we have such a \(B\). Then we must define the component of \(\alpha\), \(\alpha_A : \Hom{\sets^{\mathsf{op}}}{A}{B} \mto{} \mathcal{P}(A)\), and the only thing we have to work with is the powerset functor. To define the component \(\alpha_A\) we are given a morphism \(f : A \mto{} B\), and then the only sensible thing we can do is apply the powerset functor to it yielding \(\pow{f} : \pow{B} \mto{} \pow{A}\), which by definition computes the inverse image of \(f\) with respect to the input subset of \(B\). Now we need a subset of \(A\), and the only way to get it is by finding a subset of \(B\) in addition to \(B\) itself. Choose \(B = \{0,1\}\), then we define \(\alpha_A(f : A \mto{} B) = \pow{f}(\{1\})\). This construction uses the characteristic function on \(A\) to determine which subset to choose.

    It is easy to see that we can also define the component \(\alpha^{-1}_A : \pow{A} \mto{} \Hom{\sets^{\mathsf{op}}}{A}{B}\) by

    \[ \alpha^{-1}_A(X) = \lambda x \in A.\left\{ \begin{array}{lr} 1 & : x \in X\\ 0 & : x \notin X \end{array} \right. \]

    We can see that \(\alpha_A;\alpha^{-1}_A = \id = \alpha^{-1}_A;\alpha_A\). Hence, each \(\alpha_A\) is an isomorphism.

    Last but not least, we must show that \(\alpha\) is a natural transformation. Thus, we must prove that the following diagram commutes for any \(f : A' \mto{} A\):

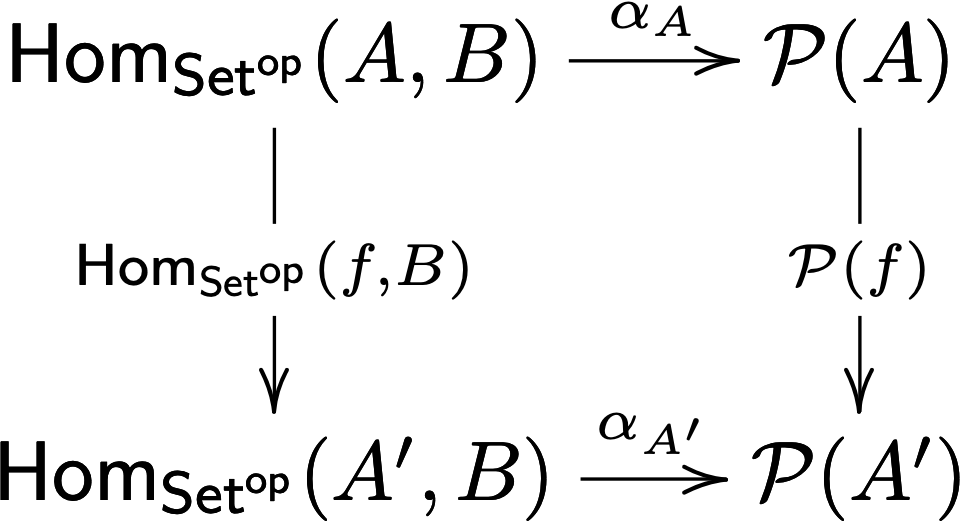
    Naturality diagram for the representation of the powerset functor.

    This follows from straightforward equational reasoning using the definitions of the respective functions in play.

  • Suppose \(A,B \in \Obj{C}\). What is a representation of the functor \(\Hom{\cat{C}}{-}{A} \times \Hom{\cat{C}}{-}{B}\)? It must be a pair \((P,\beta)\) such that \(\beta : (\Hom{\cat{C}}{-}{A} \times \Hom{\cat{C}}{-}{B}) \mto{} \Hom{C}{-}{P}\) is natural isomorphism. The structure of \(\beta\) tells us that given a pair \((f,g)\) of morphisms \(f : X \mto{} A\) and \(g : X \mto{} B\) we must produce a morphism \(h : X \mto{} P\). We have seen this pattern before in the universal property of binary products given in the introduction. Suppose \(\cat{C}\) has binary products, then take \(P = A \times B\). Then the universal property of binary products implies that \(\beta : (\Hom{\cat{C}}{-}{A} \times \Hom{\cat{C}}{-}{B}) \mto{} \Hom{C}{-}{A \times B}\) is defined to be \(\beta_{X}(f,g) = \langle f,g\rangle\). That is, the universal map of the binary product. In the opposite, we have \(\beta^{-1}_X(h) = (h;\pi_1,h;\pi_2)\). The universal property of binary products implies that these are mutual inverses.

    The previous example assumes \(\cat{C}\) has binary products, but representablity is more general than that. It actually gives a formal means of describing the universal property of binary products, and when a category has binary products. Given a category \(\cat{C}\) requiring that the functor \(\Hom{\cat{C}}{-}{A} \times \Hom{\cat{C}}{-}{B}\) is representable implies there is a representation \((P,\beta)\) that can be used to define the following morphisms:

    \[ \begin{array}{lll} \pi_1 = \mathsf{fst}(\beta^{-1}_{P}(\id_P)) \in \Hom{\cat{C}}{P}{A}\\ \pi_2 = \mathsf{snd}(\beta^{-1}_{P}(\id_P)) \in \Hom{\cat{C}}{P}{B}\\ \langle f,g \rangle = \beta_{X}(f,g) \in \Hom{\cat{C}}{X}{P}\\ \end{array} \]

    Here \(\mathsf{fst}\) and \(\mathsf{snd}\) are the projections for the cartesian product in \(\mathsf{Set}\). Now we must show the following equations hold:

    \[ \begin{array}{lll} \langle f,g \rangle;\pi_1 = f : P \mto{} A\\ \langle f,g \rangle;\pi_2 = g : P \mto{} B\\ \end{array} \]

    By definition, these are equivalent to the following fully spelled out equations:

    \[ \begin{array}{lll} \beta_{X}(f,g);\mathsf{fst}(\beta^{-1}_{P}(\id_P)) = f : P \mto{} A\\ \beta_{X}(f,g);\mathsf{snd}(\beta^{-1}_{P}(\id_P)) = g : P \mto{} B\\ \end{array} \]

    Let’s consider the former and the latter will follow similarly. Consider the naturality condition for \(\mathsf{fst}\).

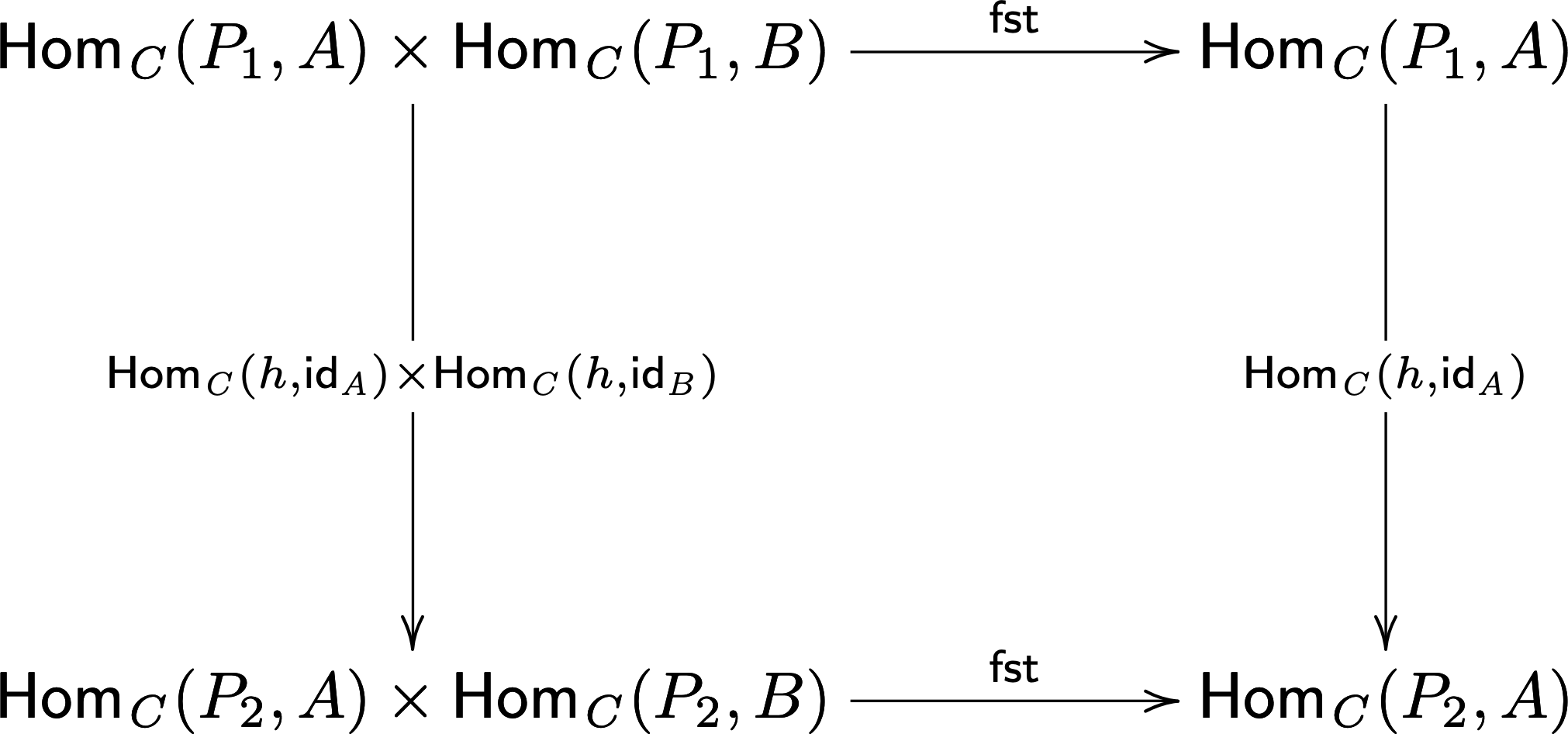
    Naturality the first project of the cartesian product in Set.

    This diagram states the following:

    \[ h;\mathsf{fst}(f,g) = f = \mathsf{fst}(h;f,h;g) \]

    Let’s pair this diagram up with the naturality diagram for \(\beta^{-1}_P\), because we apply \(\mathsf{fst}\) to this in our equation:

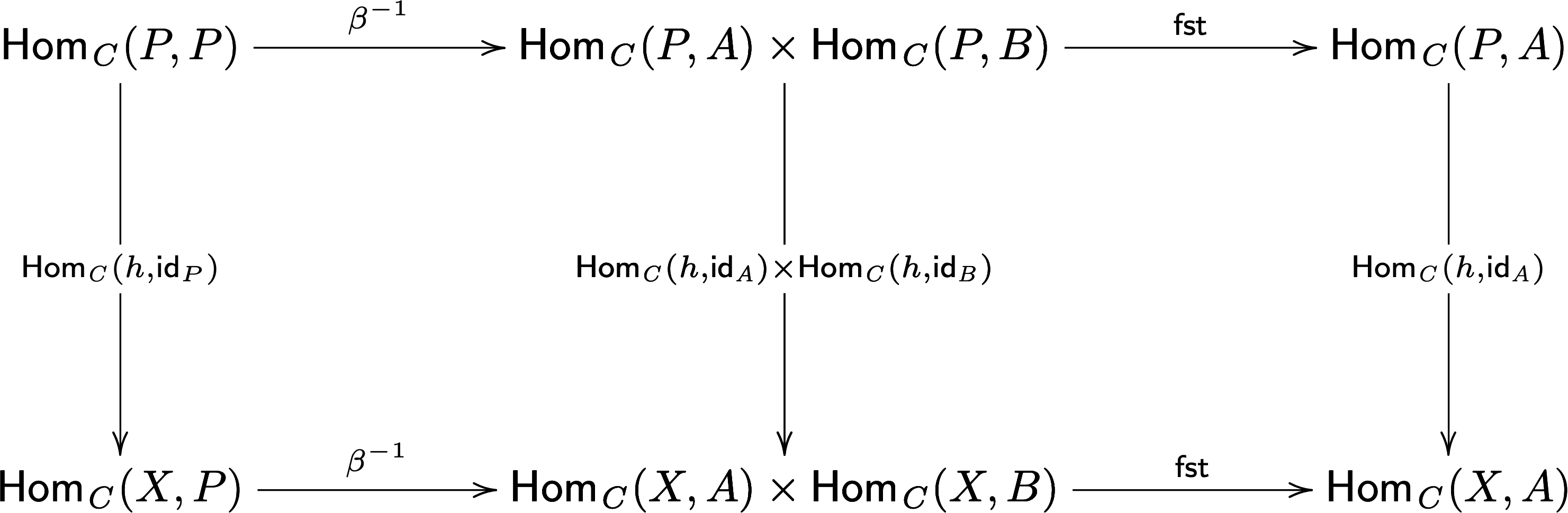
    Naturality of the representation of the product functor.

    Since we know that both of these diagrams commute we know that the outer diagram commutes. Thus, we know the following:

    \[ h;\mathsf{fst}(\beta^{-1}(p)) = \mathsf{fst}(\beta^{-1}(h;p)) \]

    This equation is exactly what we need, because our original equation we set out to prove:

    \[ \beta_{X}(f,g);\mathsf{fst}(\beta^{-1}_{P}(\id_P)) = f : P \mto{} A \]

    fits the form of \(h;\mathsf{fst}(\beta^{-1}(p))\) where we replace \(h\) with \(\beta_{X}(f,g)\) and \(p\) with \(\mathsf{id} _{ P }\). Thus, we may conclude that:

    \[ \beta_{X}(f,g);\mathsf{fst}(\beta^{-1}(\mathsf{id} _{ P })) = \mathsf{fst}(\beta^{-1}(\beta_{X}(f,g);\mathsf{id} _{ P })) = \mathsf{fst}(\beta^{-1}(\beta_{X}(f,g))) \]

    But, we also know that \(\beta\) and \(\beta^{-1}\) are mutual inverses because they form a representation with \(P\), and thus, we know that:

    \[ \mathsf{fst}(\beta^{-1}(\beta_{X}(f,g))) = \mathsf{fst}(f,g))) = f \]

    therefore proving the equation we set out to prove. The case for \(\pi_2\) is similar.

    What we have shown is that to require that a category \(\cat{ C }\) has binary products we merely ask that for every pair of objects \((A,B) \in \Obj{ C }\), the contravariant functor \(\Hom{\cat{ C }}{-}{A} \times \Hom{\cat{ C }}{-}{B} : \catop{ C } \, \mto{} \, \mathsf{Set}\) is representable which as we have shown implies the universal property of binary products. In fact, we can say that each representable functor is the universal property for the binary product the representable functor witnesses.

    A final interesting point is that the representable functor can also be seen as an interpretation of the binary products in \(\cat{ C }\) into the cartesian product in \(\mathsf{Set}\). We move from a universe without elements into a universe with elements.

  • Suppose we have a functor \(F \ottsym{:} \cat{ A } \mto{} \cat{ B }\). Now ask the question, what universal property arises from requiring the following functor to be representable?

    \[ \Hom{\mathsf{Cat}}{F \ottsym{(} - \ottsym{)}}{b} : \catop{ A } \, \mto{} \, \mathsf{Set} \]

    Representablity states that there must be a representation \((\alpha, X)\) such that:

    \[ \alpha : \Hom{\mathsf{Cat}}{F \ottsym{(} - \ottsym{)}}{b} \mto{} \Hom{\cat{ A }}{-}{X} : \catop{ A } \, \mto{} \, \mathsf{Set} \]

    is a natural isomorphism. This implies that for any morphism \(f \ottsym{:} F \ottsym{(} a \ottsym{)} \mto{} b\) there is a unique morphism \(\alpha(f) : a \, \mto{} \, X\). One thing that our previous examples have shown is that we get interesting arrows when we apply the representation bijection to the identity morphism. We can do this only for \(\alpha^{-1}\) here, which gives a morphism \(\alpha^{-1}(\mathsf{id} _{ X }) : F \ottsym{(} X \ottsym{)} \, \mto{} \, b\); the morphisms arising from the application of the representation bijection to the identity are called universal arrows.

    The universal arrow \(\alpha^{-1} \ottsym{(} \mathsf{id} _{ X } \ottsym{)} \ottsym{:} F \ottsym{(} X \ottsym{)} \mto{} b\) implies that \(X\) must depend on the object \(b\). However, \(X \in \Obj{ A }\) and \(b \in \Obj{ B }\), this leads us to think of \(X\) as \(G \ottsym{(} b \ottsym{)}\) for some functor \(G \ottsym{:} \cat{ B } \mto{} \cat{ A }\). Thus, we have a bijection:

    \[ \alpha : \Hom{B}{F \ottsym{(} - \ottsym{)}}{b} \mto{} \Hom{\cat{ A }}{-}{G(b)} : \catop{ A } \, \mto{} \, \mathsf{Set} \]

    such that there is an universal arrow \(\alpha^{-1} \ottsym{(} \mathsf{id} _{ G \ottsym{(} b \ottsym{)} } \ottsym{)} \ottsym{:} F \ottsym{(} G \ottsym{(} b \ottsym{)} \ottsym{)} \mto{} b\), and for any morphism \(f \ottsym{:} F \ottsym{(} a \ottsym{)} \mto{} b\) we have a unique morphism \(\alpha \ottsym{(} f \ottsym{)} \ottsym{:} a \mto{} G \ottsym{(} b \ottsym{)}\). But, how are these morphisms related? That is, what is the universal property implied by \(\alpha\)? This is where the naturality property comes in.

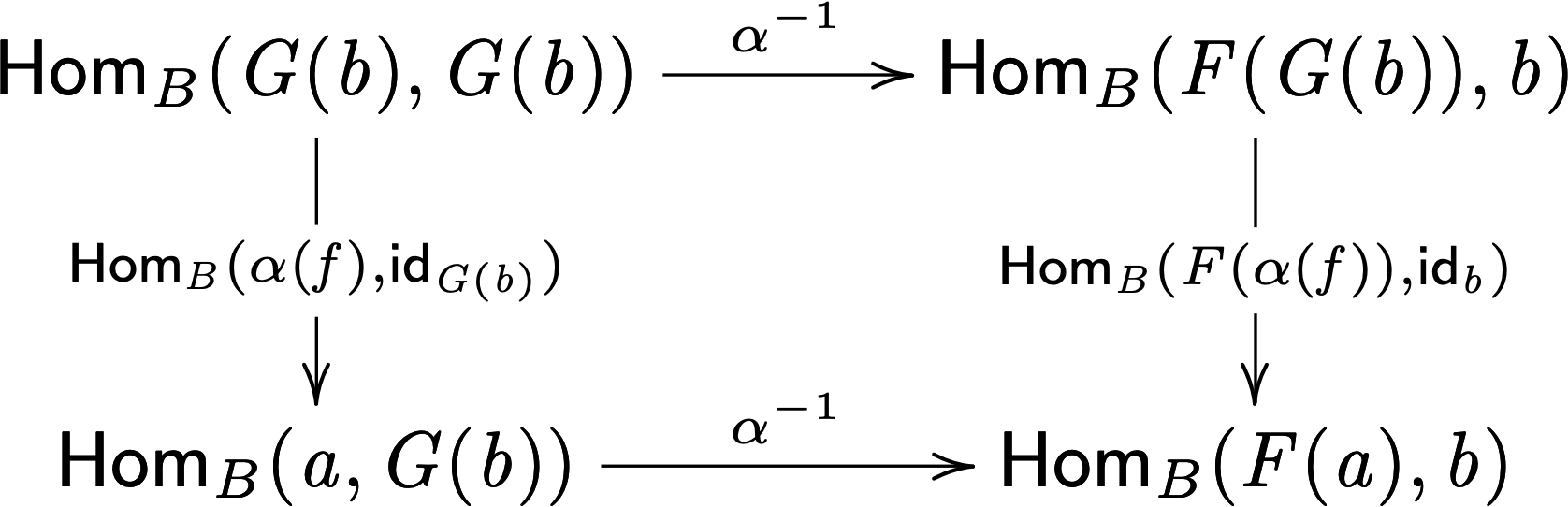
    Naturality diagram for the representation of the left-adjoint functor.

    Following the previous example we plug \(\alpha \ottsym{(} f \ottsym{)}\) into the naturality diagram for the universal arrow \(\alpha^{-1} \ottsym{(} \mathsf{id} _{ G \ottsym{(} b \ottsym{)} } \ottsym{)}\). Tracing the identity arrow around this diagram implies that the following equation holds:

    \[ F \ottsym{(} \alpha \ottsym{(} f \ottsym{)} \ottsym{)} \ottsym{;} \alpha^{-1} \ottsym{(} \mathsf{id} _{ G \ottsym{(} b \ottsym{)} } \ottsym{)} \ottsym{;} \mathsf{id} _{ b } = \alpha^{-1} \ottsym{(} \alpha \ottsym{(} f \ottsym{)} \ottsym{;} \mathsf{id} _{ G \ottsym{(} b \ottsym{)} } \ottsym{;} \mathsf{id} _{ G \ottsym{(} b \ottsym{)} } \ottsym{)} \]

    and as we can see we can drop all the identity compositions to obtain:

    \[ F \ottsym{(} \alpha \ottsym{(} f \ottsym{)} \ottsym{)} \ottsym{;} \alpha^{-1} \ottsym{(} \mathsf{id} _{ G \ottsym{(} b \ottsym{)} } \ottsym{)} = \alpha^{-1} \ottsym{(} \alpha \ottsym{(} f \ottsym{)} \ottsym{)} = f \]

    This is equivalent to the diagram:

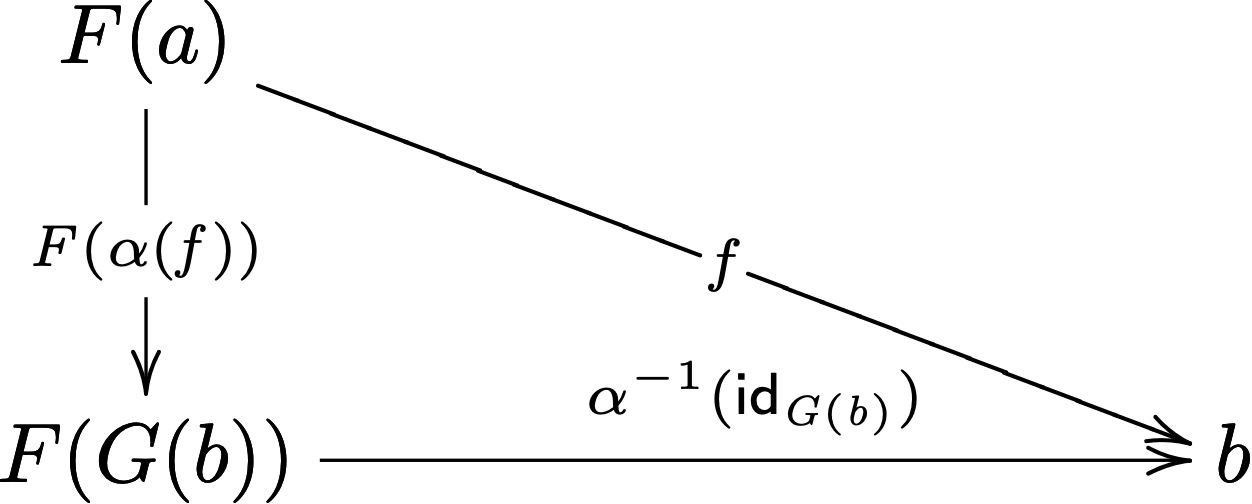
    Universal property for a left-adjoint functor using the representation.

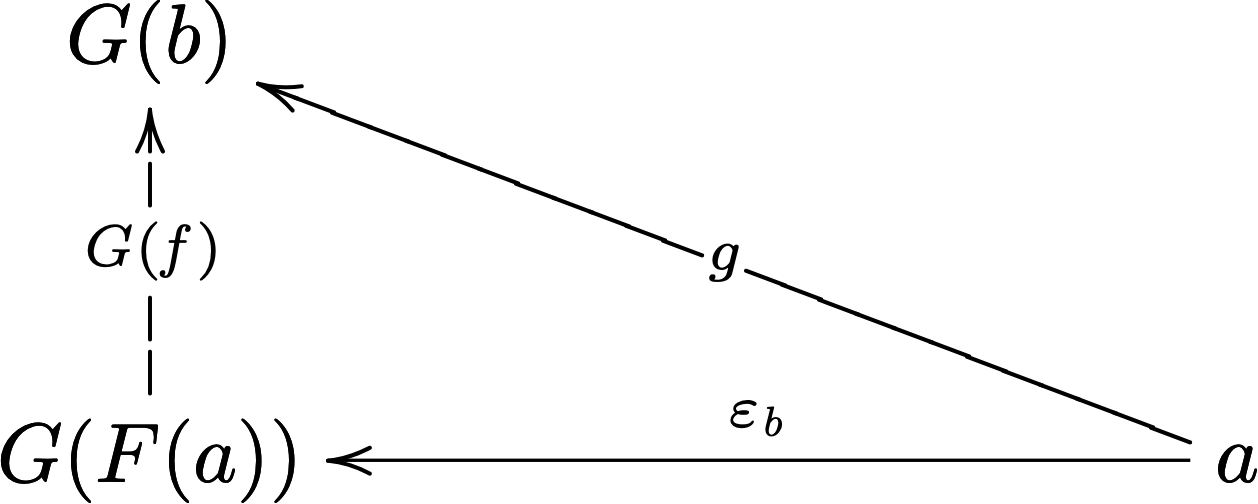
    We can now capture this line of reasoning as an abstract universal property:

    • For a functor \(F \ottsym{:} \cat{ A } \mto{} \cat{ B }\), there is a functor \(G \ottsym{:} \cat{ B } \mto{} \cat{ A }\) where for any object \(b \in \Obj{ B }\), there is a universal arrow \(\varepsilon_{b} : F \ottsym{(} G \ottsym{(} b \ottsym{)} \ottsym{)} \, \mto{} \, b\) such that for every morphism \(f \ottsym{:} F \ottsym{(} a \ottsym{)} \mto{} b\) there is a unique morphism \(g \ottsym{:} a \mto{} G \ottsym{(} b \ottsym{)}\) making the following diagram commute:

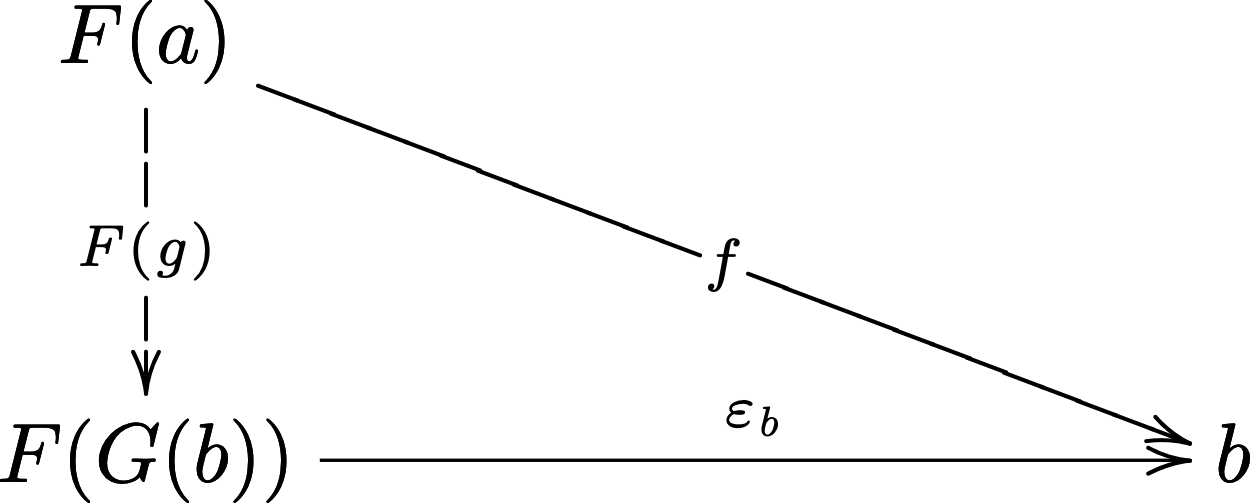
      Universal property for a left-adjoint functor.

    If for a functor \(F \ottsym{:} \cat{ A } \mto{} \cat{ B }\) there is a functor \(G \ottsym{:} \cat{ B } \mto{} \cat{ A }\) satisfying the previous universal property we say \(F\) is left adjoint to the functor \(G\). This is often denoted by \(F \dashv G\).

    Given there are left adjoints you might ask if there are right adjoints. In fact there are, and they have the following universal property:

    • For a functor \(G \ottsym{:} \cat{ B } \mto{} \cat{ A }\), there is a functor \(F \ottsym{:} \cat{ A } \mto{} \cat{ B }\) where for any object \(a \in \Obj{ A }\), there is a universal arrow \(\eta_{a} : a \, \mto{} \, G \ottsym{(} F \ottsym{(} a \ottsym{)} \ottsym{)}\) such that for every morphism \(g \ottsym{:} a \mto{} G \ottsym{(} b \ottsym{)}\) there is a unique morphism \(f \ottsym{:} F \ottsym{(} a \ottsym{)} \mto{} b\) making the following diagram commute:

      Universal property for a right-adjoint functor.

      We leave deriving the previous universal property as an exercise. If for a functor \(G \ottsym{:} \cat{ B } \mto{} \cat{ A }\) there is a functor \(F \ottsym{:} \cat{ A } \mto{} \cat{ B }\) satisfying the previous universal property we say \(G\) is right adjoint to the functor \(F\). Again, we denote this by \(F \dashv G\).

    There is a lot we can say about adjoint functors (or adjunctions for short), but we leave that for a later time.

  • Suppose we have a partially-ordered monoid \((M,*, e, \leq)\).

References

Awodey, S. 2006. Category Theory. Oxford Logic Guides. Ebsco Publishing. https://books.google.com/books?id=IK\_sIDI2TCwC.

Leave a comment by sending me an Email