Coalgebras, Comonads, and Distributive Laws

In my current project investigating the categorical semantics of attack trees we are using distributive laws to compose comonads that model various structural rules – weakening, contraction, exchange, etc – in linear logic. During the QA section of my talk at Linear logic, mathematics and computer science – see my post on my talk and the workshop for more details – Paul-André Melliès suggested using adjunctions to compose the structural rules instead of distributive laws for the obvious reason that they really compose as opposed to monads/comonads. I told him that I did try to this initially, but was not able to get it working. He was nice enough to talk with me a bit and gave me some hints to how it works which are based on a paper of his.

Instead of just looking up the details in his paper I wanted to see if I could recreate his result with his hints. I often do this for learning purposes. So that’s what I did during my flight back from France. I figured why not make it a blog post. Keep in mind that this result is due to Paul-André, but I had a lot of fun recreating his steps.

I plan to write a follow up post describing how this result can be used to to create various adjoint models of linear logic, but here we show that when we have two comonads on a category with a distributive law, then those comonads in addition to their composition can be decomposed into a composition of adjunctions between their coalgebras.

Suppose

(k, ε, δ)

is a comonad on a category

L

. Then it is well known that it can be decomposed into the following adjunction: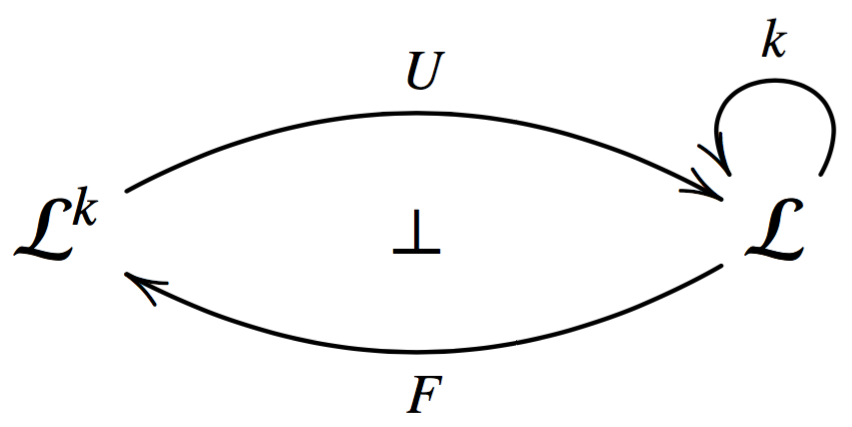

where $U : L^{k} \to L$ is the forgetful functor, $F : L \to L^{k}$ is the free functor, and $k = U F : L \to L$ .

Now suppose we have the following adjunctions: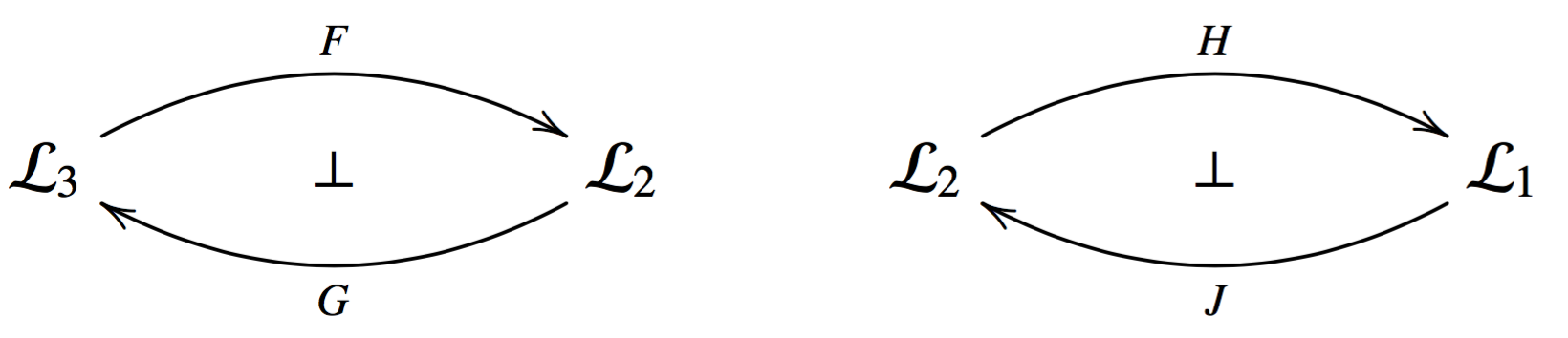

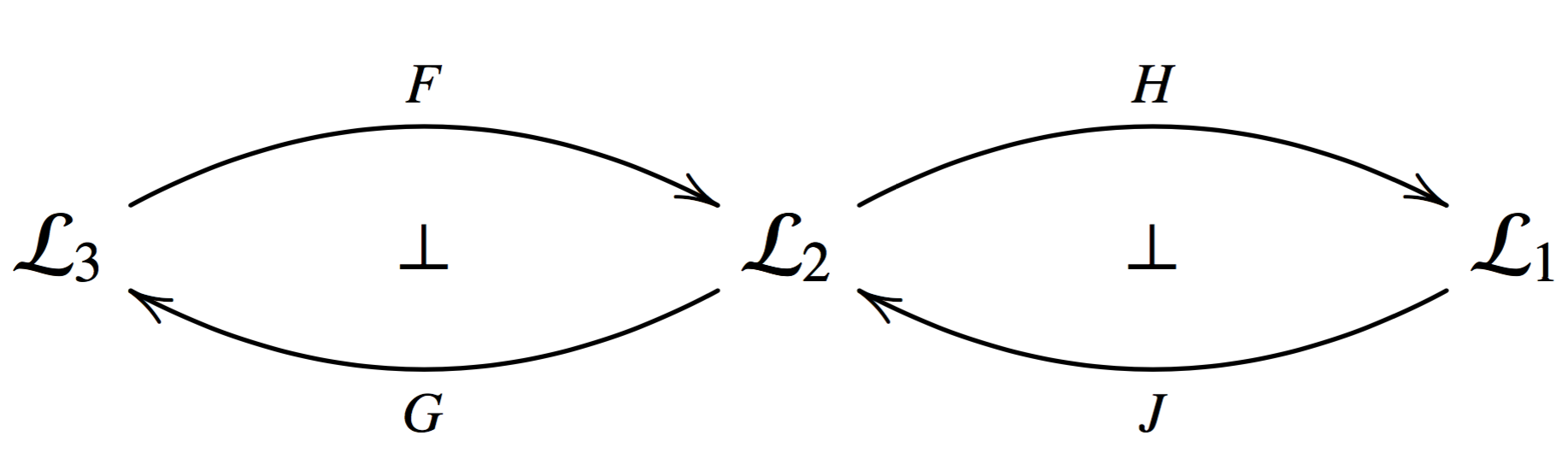
Then they can be composed into the adjunction:

Keep in mind that this gives rise to a comonad $H F G J : L_{1} \to L_{1}$ .

We are going to use these two facts to compose comonads using adjunctions. Suppose we have the comonads $(k_{1}, ε^{1}, δ^{1})$ and $(k_{2}, ε^{2}, δ^{2})$ both on a category $L$ with a distributive law – distributive laws for comonads are defined to be the opposite of the distributive laws for monads – $dist : k_{2} k_{1} \to k_{1} k_{2}$ . Thus, making $k_{2} k_{1} : L \to L$ a comonad.

Then we can decompose

k_{1}

into a an adjunction: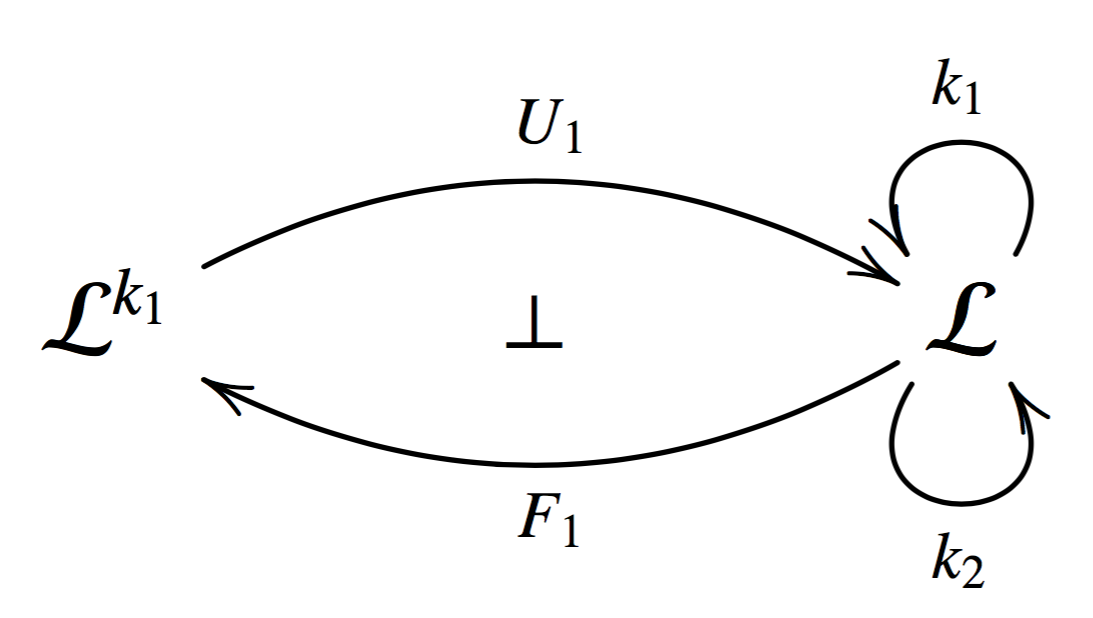

Here we know that $k_{1} = U_{1} F_{1} : L \to L$ , but we also know something about $k_{2}$ . We can extend it to a comonad on $L^{k_{1}}$ .

First, we define the functor

{\tilde{k}}_{2} : L^{k_{1}} \to L^{k_{1}}

to send objects

(A, h_{A})

(k_{2} A, h_{A}^{'})

, where

h_{A}^{'} := k_{2} A \to^{k_{2} h_{A}} k_{2} k_{1} A \to^{{dist}_{A}} k_{1} k_{2} A

, and to send morphisms

f : (A, h_{A}) \to (B, h_{B})

to the morphism

k_{2} f : (k_{2} A, h_{A}^{'}) \to (k_{2} B, h_{B}^{'})

. We must show that

k_{2} f : k_{2} A \to k_{2} B

is a coalgebra morphism, but the following diagram commutes: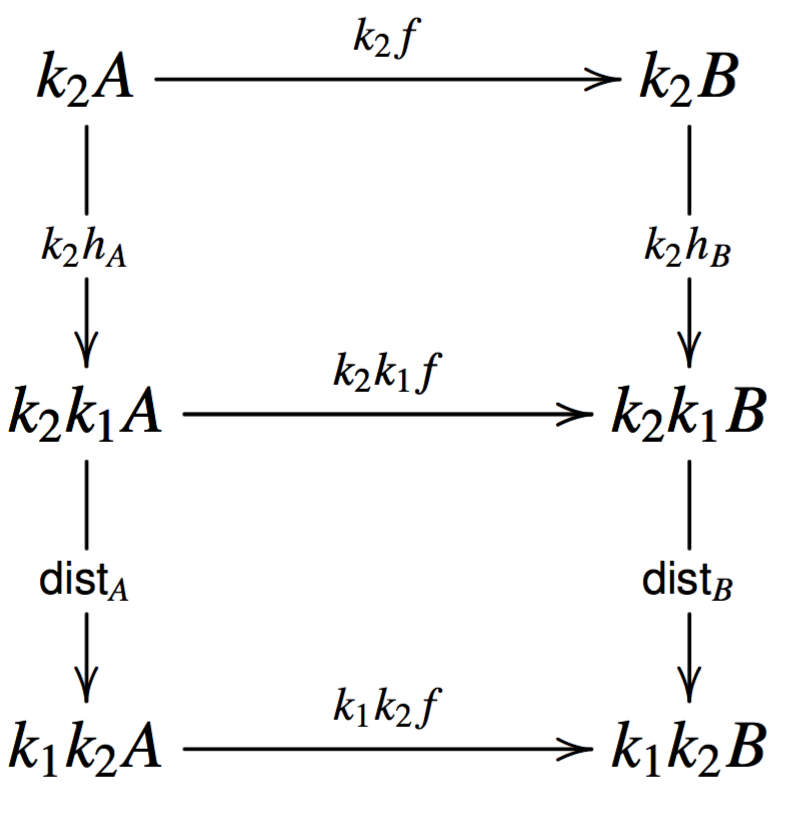

The top diagram commutes because $f$ is a coalgebra morphism and the bottom diagram commutes by naturality of $dist$ . Since the morphism part of ${\tilde{k}}_{2}$ is defined using the functor $k_{2}$ we know ${\tilde{k}}_{2}$ will respect composition and identities.

We now must show that

{\tilde{k}}_{2}

is a comonad. The natural transformation

\tilde{ε^{2}} : {\tilde{k}}_{2} \to Id

has components

{\tilde{ε^{2}}}_{(A, h_{A})} = ε_{A}^{2} : {\tilde{k}}_{2} (A, h_{A}) \to (A, h_{A})

. We must show that

ε_{A}^{2}

is a coalgebra morphism between

{\tilde{k}}_{2} (A, h_{A}) = (k_{2} A, k_{2} h_{A}; {dist}_{A})

and

(A, h_{A})

, but this follows from the following diagram: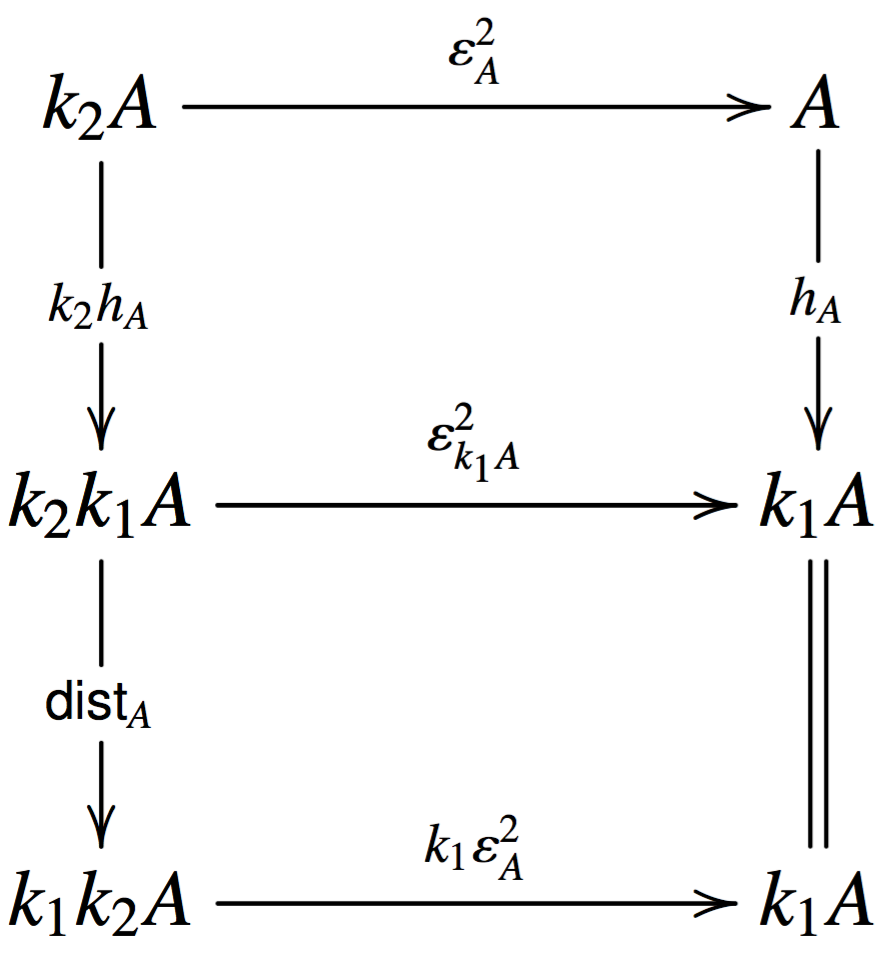

The top diagram commutes by naturality of $ε^{2}$ and the bottom diagram commutes by the conditions of the distributive law. Naturality for $\tilde{ε^{2}}$ easily follows from the fact that it is defined to be $ε_{2}$ .

The natural transformation

\tilde{δ^{2}} : \tilde{k_{2}} \to \tilde{k_{2}} \tilde{k_{2}}

has components

{\tilde{δ^{2}}}_{(A, h_{A})} = δ_{A}^{2} : \tilde{k_{2}} (A, h_{A}) \to \tilde{k_{2}} \tilde{k_{2}} (A, h_{A})

. Just as above we must show that

δ_{A}^{2} : k_{2} A \to k_{2}^{2} A

is a coalgebra morphism between

\tilde{k_{2}} (A, h_{A}) = (k_{2} A, k_{2} h_{A}; {dist}_{A})

and

\tilde{k_{2}} \tilde{k_{2}} (A, h_{A}) = (k_{2}^{2} A, k^{2} h_{A}; k_{2} {dist}_{A}; {dist}_{k_{2} A})

, but this follows from the following diagram: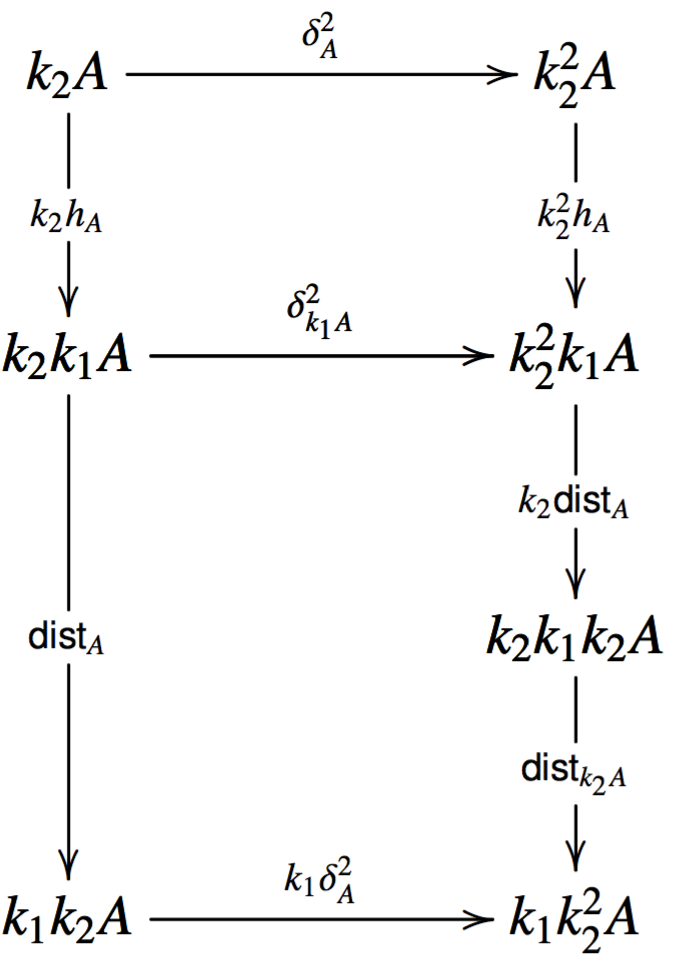

The top diagram commutes by naturality of $δ^{2}$ and the bottom diagram commutes by the conditions of the distributive law.

It is now easy to see that $\tilde{ε^{2}}$ and $\tilde{δ^{2}}$ make $\tilde{k_{2}}$ a comonad on $L^{k_{1}}$ , because the conditions of a comonad will be inherited from the fact that $ε^{2}$ and $δ^{2}$ define a comonad on $L$ .

At this point we have arrived at the following situation:

Since we have a comonad

\tilde{k_{2}} : L^{k_{1}} \to L^{k_{1}}

we can form the following adjunction:

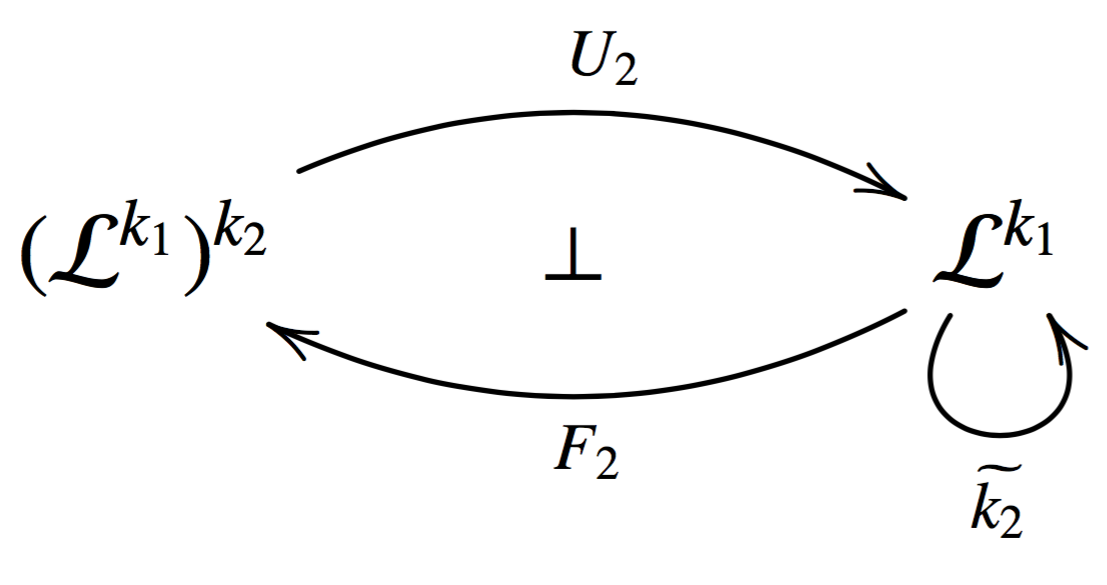
The functor $F_{2} (A, h_{A}) = (\tilde{k_{2}} (A, h_{A}), {\tilde{δ^{2}}}_{(A, h_{A})})$ is the free functor, and $U_{2} (A, h_{A}) = A$ is the forgetful functor. Thus, we can think of $(L^{k_{1}})^{k_{2}}$ as the world with all the structure of $L$ extended with all of the structure $k_{1}$ brings and all the structure $k_{2}$ brings. That is, $(L^{k_{1}})^{k_{2}}$ is the algebras of $k_{2} k_{1} : L \to L$ .

We can see that the previous two adjunctions compose:

Thus, we have a comonad

U_{1} U_{2} F_{2} F_{1} : L \to L

. Chasing an object through this comonad yields the following:

\begin{array}{lll} U_{1} U_{2} F_{2} F_{1} A & = & U_{1} U_{2} F_{2} (k_{1} A, δ_{A}^{1}) \\ = & U_{1} U_{2} (\tilde{k_{2}} ((k_{1} A, δ_{A}^{1})), {\tilde{δ^{2}}}_{(k_{1} A, δ_{A}^{1})}) \\ = & U_{1} U_{2} ((k_{2} k_{1} A, k_{2} δ_{A}^{1}; {dist}_{k_{1} A}), {\tilde{δ^{2}}}_{(k_{1} A, δ_{A}^{1})}) \\ = & U_{1} (k_{2} k_{1} A, k_{2} δ_{A}^{1}; {dist}_{k_{1} A}) \\ = & k_{2} k_{1} A \end{array}

Therefore, the above adjunction gives back the composition $k_{2} k_{1} : L \to L$ .

This result only works because we have a distributive law, but the distributive law is only used in the the definition of the structural map of the coalgebras. This result reveals a means that will allow us to abandon distributive laws in favor of adjunctions in the spirit of Benton’s LNL models, however, doing so comes with some different difficulties. Stay tuned!